Trong chủ đề này chúng ta sẽ tìm hiểu
- Tương quan là gì?
- So sánh hệ số Pearson và Spearman
- Các mối quan hệ phi tuyến khác
Tương quan là gì?
Hệ số tương quan đo lường mức độ mà hai biến số có xu hướng thay đổi cùng nhau. Hệ số mô tả cả cường độ và hướng của mối quan hệ. Phần mềm Minitab cung cấp hai phân tích tương quan khác nhau:
Tương quan thời điểm sản phẩm Pearson
Tương quan Pearson đánh giá mối quan hệ tuyến tính giữa hai biến liên tục. Một mối quan hệ là tuyến tính khi sự thay đổi của một biến có liên quan đến sự thay đổi tỷ lệ của biến kia.
Ví dụ: bạn có thể sử dụng mối tương quan Pearson để đánh giá xem liệu việc tăng nhiệt độ tại cơ sở sản xuất của bạn có liên quan đến việc giảm độ dày lớp phủ chocolate hay không.
Tương quan thứ tự Spearman
Mối tương quan Spearman đánh giá mối quan hệ đơn điệu giữa hai biến liên tục hoặc thứ tự. Trong mối quan hệ đơn điệu, các biến số có xu hướng thay đổi cùng nhau nhưng không nhất thiết phải ở mức không đổi. Hệ số tương quan Spearman dựa trên các giá trị được xếp hạng cho từng biến thay vì dữ liệu thô.
Tương quan Spearman thường được sử dụng để đánh giá các mối quan hệ liên quan đến các biến thứ tự.
Ví dụ:
Bạn có thể sử dụng mối tương quan Spearman để đánh giá xem thứ tự nhân viên hoàn thành bài kiểm tra có liên quan đến số tháng họ đã làm việc hay không.
Việc kiểm tra mối quan hệ giữa các biến bằng biểu đồ phân tán luôn là một ý tưởng hay. Các hệ số tương quan chỉ đo lường các mối quan hệ tuyến tính (Pearson) hoặc đơn điệu (Spearman). Các mối quan hệ khác là có thể.
So sánh hệ số Pearson và Spearman
Hệ số tương quan Pearson và Spearman có thể có giá trị từ −1 đến +1. Để hệ số tương quan Pearson là +1, khi một biến tăng thì biến kia tăng một lượng nhất quán. Mối quan hệ này tạo thành một đường thẳng hoàn hảo. Hệ số tương quan Spearman cũng là +1 trong trường hợp này.
Nếu mối quan hệ là một biến tăng khi biến kia tăng nhưng số lượng không nhất quán thì hệ số tương quan Pearson dương nhưng nhỏ hơn +1. Hệ số Spearman vẫn bằng +1 trong trường hợp này.
Khi một mối quan hệ là ngẫu nhiên hoặc không tồn tại thì cả hai hệ số tương quan đều gần như bằng 0.
Nếu mối quan hệ là một đường hoàn hảo cho mối quan hệ giảm dần
-> Cả hai hệ số tương quan đều là −1.
Nếu mối quan hệ là một biến giảm khi biến kia tăng nhưng số lượng không nhất quán thì hệ số tương quan Pearson âm nhưng lớn hơn −1. Hệ số Spearman vẫn bằng −1 trong trường hợp này.
Các giá trị tương quan −1 hoặc 1 ngụ ý một mối quan hệ tuyến tính chính xác, giống như mối quan hệ giữa bán kính và chu vi của một hình tròn. Tuy nhiên, giá trị thực sự của các giá trị tương quan nằm ở việc định lượng các mối quan hệ chưa hoàn hảo. Việc phát hiện ra rằng hai biến có mối tương quan thường cung cấp thông tin cho phân tích hồi quy nhằm cố gắng mô tả loại mối quan hệ này nhiều hơn.
Các mối quan hệ phi tuyến tính khác
Hệ số tương quan Pearson chỉ đo lường mối quan hệ tuyến tính. Hệ số tương quan Spearman chỉ đo lường các mối quan hệ đơn điệu. Vì vậy, một mối quan hệ có ý nghĩa có thể tồn tại ngay cả khi hệ số tương quan bằng 0. Kiểm tra biểu đồ phân tán để xác định dạng của mối quan hệ.
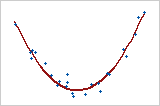
Biểu đồ này cho thấy một mối quan hệ rất mạnh mẽ. Hệ số Pearson và hệ số Spearman đều xấp xỉ bằng 0.
Tìm hiểu thêm về Phần mềm thống kê Minitab ▶ Tham gia khóa học của chúng tôi!
Ngoài ra, nếu có nhu cầu tham khảo giá mua bản quyền Minitab, vui lòng liên hệ ngay với Minitab Việt Nam để được nhận báo giá và tư vấn về sản phẩm kỹ hơn:
Hotline: 024 6682 0511
Email: sale@minitabvietnam.com
Website: https://minitabvietnam.com/
Add: Tầng 4, Tòa nhà N01-T4, Khu Đoàn Ngoại Giao, P. XuânTảo, Q. Bắc Từ Liêm, TP. Hà Nội